Subway Surfers

One day I was playing Subway Surfers, and I couldn't help but feel that coins were more heavily dispersed amongst the edge rows. Now if you're not familiar with Subway Surfers, it's got power-ups, and the one I'm talking about is called a jetpack. The jetpack raises the player above all the obstacles and leaves the players to follow a path of coins. These coins transfer between the 3 lanes a player can run in, and one can't help but think, "If I couldn't switch lanes, which one would give me the most coins?"

Are coins equally distributed across all three lanes in Subway Surfer? If one were to deploy a jetpack, and could only pick a single lane to remain in for the duration of the jetpack's fuel reserves, which lane would a clever man choose? What statistical methods might that wise woman employ to make such a determination? I set out seeking the source of this wisdom, and found Master Markov. It is his chains that guide me now through The Subway.

Now, Markov Chains are a way to calculate probability for things that don't stop. Basically, one takes a representation of the movement between states as a matrix transformation and performs an integral on it, I think. I've never taken a statistics course.

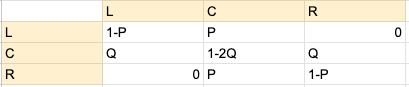
The X axis in the matrix representation above, Left (L), Center (C), and Right (R), are the starting positions, and the Y axis represents the next position. The number in each cell represents the probability of going from X to Y. It's clear we make a few assumptions here, notably that movement from the right column is equivalent to movement from the left column. Also one rule to follow the game logic, is that one cannot traverse directly from the right to the left column and vice versa.

Taking this transformation matrix and performing the integration we get these three equations:

Which underwhelmingly simplifies to $P=Q$. This means, as long as the probability of moving from an edge lane to the center is the same as moving from the center to an edge lane, the distribution should approach equal as the number of coins grows.